LG Aimers에서 KAIST 신진우 교수님 강의를 듣고 정리한 내용입니다.
틀린 부분이 있다면 댓글 부탁드립니다!
1. Determinant and Trace
(1) Determinant

2 x 2 행렬 A에 대해서 역행렬이 존재하는지 알기 위해서 determinant를 구해본다.
determinant가 0이 아니라면 invertible하다.
2 x 2 행렬에서는 공식처럼 쉽게 역행렬을 구할 수 있다.
더 큰 행렬에 대해서는 Gaussian elimination 방법으로 역행렬을 구한다.

- determinant를 구하는 방법 중 하나로 Laplace expansion (라플라스 전개)가 있다.

행 확장이나 열 확장이나 결과는 동일하므로, 더 편한 방법을 사용하면 된다.
(2) determinant theorm
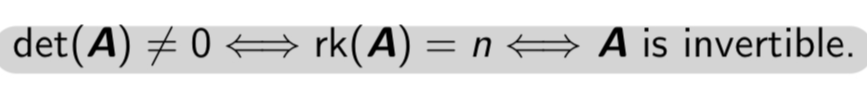
rk(A)는 A에 대한 rank (Column space의 차원 수)이다.
- determinant에 대한 성질은 다음과 같다.

determinant는 곱셈에 대해서 분리 가능하다는 점이 특징이다.
또한, (5)에서 삼각행렬에 대한 determinant 공식인데, 이는 당연하게도 대각행렬에서도 성립한다.
(3) Trace (대각합)
행렬의 대각 원소에 대한 합을 의미한다.

determinant가 곱셈에 대한 분해가 가능하다는 특징이 있었다면, trace는 덧셈에 대한 분해가 가능하다는 특징이 있다.
determinant와 trace는 고유값 분해에서 각각 고유값의 곱과 고유값의 합과 같다.
2. Eigenvalues and Eigenvectors
(1) 고유값과 고유 벡터

특성 방정식에 대한 determinant가 0이어야 한다.
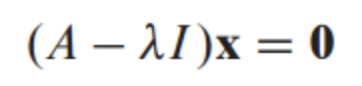
그 이유는 적어둔 것과 같이 x가 영벡터가 아니라는 가정에서 특성 방정식이 역행렬을 가지지 않아야지만 해를 가질 수 있기 때문이다.
예를 들어,

이 결과를 통해 eigenvector는 하나만 존재하는 것이 아님을 알 수 있다.
(2) 특징
행렬 A가 n개의 서로 다른 고유값을 가진다면, 고유 벡터들은 linearly independent하다.

1. determinant에서 언급한 바와 같이, determinant와 trace는 고유값 분해에서 각각 고유값의 곱과 고유값의 합과 같다.
3. Cholesky Decomposition
주어진 행렬이 어떤 작은 행렬 두 개의 곱으로 나타낼 때 사용한다.
조건은 Positive-semi definite 행렬이어야 한다는 점이다. 그 기저에는 대칭행렬이라는 조건이 있다.

행렬 A에 대해서 숄레스키 분해를 하면 다음과 같고, L을 a 값에 관하여 구할 수 있다.

4. Eigen-decomposition and Diagonalization
(1) Diagonal Matrix and Diagonalization
대각행렬은 대각선에만 0이 아닌 수가 있고 나머지에는 0을 가지는 행렬이다.
이러한 대각행렬은 determinant가 대각선 원소들의 곱과 같고, 행렬의 k승수는 대각원소의 k 승수와 같다.
또한 역행렬은 원소의 역수와 같다.

어떤 행렬이 diagonalizable 하다는 것은 행렬이 n개의 선형 독립인 고유벡터를 가진다는 것과 같은 의미이다.
Orthogonally diagonalizable 하다는 뜻은 행렬과 전치행렬의 곱이 항등행렬임을 의미하기 때문에, 위와 같이 나타낼 수 있다.
행렬의 고유벡터들로 이루어진 행렬이 직교행렬이며, 모든 대칭행렬은 orthogonally diagonalizable하다.
(2) Power of Diagonalization

5. Singular Vector Decomposition
고유값 분해는 정방행렬에서만 가능했다면, 특이값 분해는 고유값 분해가 확장된 방법이다.
1) 대칭행렬은 아니지만 정방행렬인 경우
2) 대칭행렬도, 정방행렬도 아닌 경우
이때, 행렬의 전치행렬과 행렬의 곱, 행렬과 행렬의 전치행렬의 곱이 정방행렬임을 이용한다.
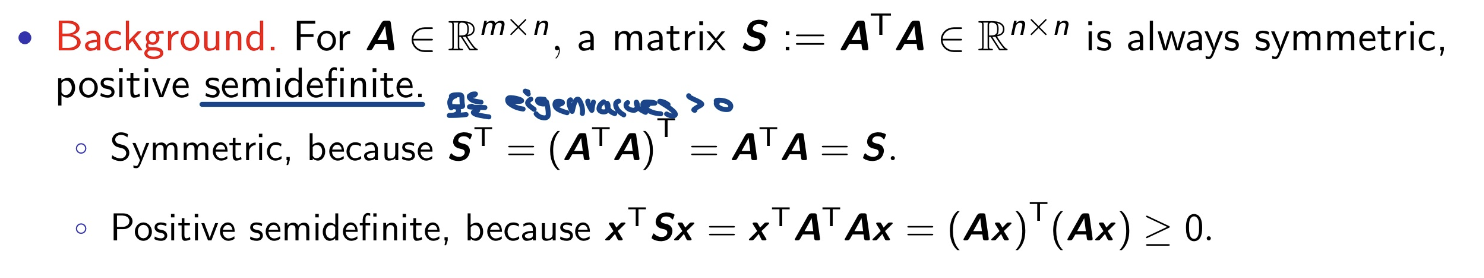
특이값 분해를 정리하면 다음과 같다.

1. 행렬을 summarize 하는 방법 : determinants, eigenvalues
2. 행렬을 분해하는 방법 : Cholesky decomposition, diagonalization, Singular value decomposition
'Artificial Intelligence > LG Aimers' 카테고리의 다른 글
| [ LG Aimers ] 『품질 경영』 Part 1. 품질경영 개론 (1) | 2024.08.06 |
|---|---|
| [ LG Aimers ] 『Mathematics for AI』 Part 3. Principal Component Analysis (1) | 2024.07.22 |
| [ LG Aimers ] 『AI 윤리』 Part 2. AI Ethics + Part 3. 세계적인 데이터 과학자가 되는 방법 (0) | 2024.07.11 |
| [ LG Aimers ] 『AI 윤리』 Part 1. 데이터 분석과 AI학습에서 유의할 점 (0) | 2024.07.11 |