Punch!

1. 문제 설명

철수와 동생은 롤케이크를 나눠 먹으려고 한다.

두 사람은 롤케이크 길이, 토핑의 개수보다 토핑 종류를 더 중요하게 생각한다.

topping 배열이 주어졌을 때, "동일한 가짓수의 토핑"을 나눠 먹을 수 있도록 하는 방법의 가짓수를 반환하라.

예를 들어, [1, 2, 1, 3, 1, 4, 1, 2] 토핑은 [1, 2, 1, 3], [1, 4, 1, 2] 또는 [1, 2, 1, 3, 1], [4, 1, 2]로 나눌 수 있으므로, 총 2가지이다.

[1, 2, 3, 1, 4]는 어떻게 나누든 공평한 토핑의 종류를 가질 수 없으므로, 0이다.

2. 코드

(1) 1차 시도

def solution(topping):
    answer = 0
    
    for i in range(1, len(topping)):
        a = topping[:i]
        b = topping[i:]
        
        if len(set(a)) == len(set(b)):
            answer += 1
    
    return answer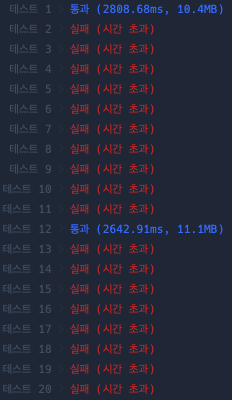

(2) 2차 시도

from collections import Counter

def solution(topping):
    topping_dict = Counter(topping)
    topping_set = set()
    answer = 0
    
    for i in topping:
        topping_dict[i] -= 1
        topping_set.add(i)
        
        if topping_dict[i] == 0:
            topping_dict.pop(i)
        
        if len(topping_set) == len(topping_dict):
            answer += 1
    
    return answer

3. 설명

배열 슬라이싱이 $O(N)$이 걸려서, 결국 $O(N^2)$ 수행시간이 걸리게 된다. 그래서 시간 초과가 났던 것이다ㅜ

슬라이싱을 안 하고, 한번의 검토로 기준선 앞, 뒤를 모두 검토할 수 있는 방식으로 다시 코드를 짰다.

Counter dictionary를 사용해서 토핑 종류에 대한 개수를 저장하고, 기준 앞쪽에 대해서 원소를 하나씩 지워나간다.

그러면서 집합에 넣어서 unique한 원소들의 개수를 구한다.

topping_set과 topping_dict 길이가 같다면 answer + 1 해준다.

1. 문제 설명

사전에 알파벳 모음 'A', 'E', 'I', 'O', 'U'만을 사용하여 만들 수 있는, 길이 5 이하의 모든 단어가 수록되어 있다.

사전에서 첫 번째 단어는 "A"이고, 그다음은 "AA"이며, 마지막 단어는 "UUUUU"이다.

단어 하나 word가 매개변수로 주어질 때, 이 단어가 사전에서 몇 번째 단어인지 반환하라.

예)

"AAAAE" → 6

"AAAE" → 10

"I" → 1563

"EIO" → 1189

2. 코드

from itertools import product

def solution(word):
    dictionary = ["".join(list(j)) for i in range(1, 6) for j in product(['A', 'E', 'I', 'O', 'U'], repeat=i)]
    dictionary = sorted(dictionary)
    
    return dictionary.index(word) + 1

3. 설명

사전 순으로 배열은 sorted 함수로 자동 배열할 수 있어서, 이 문제의 핵심은 사전에 들어갈 요소들을 구성하는 데에 있다.

from itertools import product를 불러와서 길이 5 이하로 구성할 수 있는 조합 모두를 구한다.

예를 들어서 다음과 같은 경우에는 repeat=2 이므로 길이가 2인 모든 조합의 수를 구한다.

A = [1,2,3]
list(itertools.product(A, repeat=2))

[(1, 1), (1, 2), (1, 3), (2, 1), (2, 2), (2, 3), (3, 1), (3, 2), (3, 3)]

따라서, 문제에서는 가변길이이므로 repeat=i를 두고, i를 for 문으로 1부터 5까지 반복하도록 한다.

[ j for i in range(1, 6) for j in product(['A', 'E', 'I', 'O', 'U'], repeat=i) ]

이렇게 했을 때 결과는 다음과 같다.

- 길이 1 : ('A',), ('E',), ('I',), ('O',), ('U',)

- 길이 2 : ('A', 'A'), ('A', 'E'), ('A', 'I'), ('A', 'O'), ('A', 'U'), ('E', 'A'), ('E', 'E'), ('E', 'I'), ('E', 'O'), ('E', 'U'), ('I', 'A'), ('I', 'E'), ('I', 'I'), ('I', 'O'), ('I', 'U'), ('O', 'A'), ('O', 'E'), ('O', 'I'), ('O', 'O'), ('O', 'U'), ('U', 'A'), ('U', 'E'), ('U', 'I'), ('U', 'O'), ('U', 'U')

- 길이 3 : ('A', 'A', 'A'), ('A', 'A', 'E'), ('A', 'A', 'I'), ('A', 'A', 'O'), ('A', 'A', 'U'), ('A', 'E', 'A'), ('A', 'E', 'E'), ('A', 'E', 'I'), ('A', 'E', 'O'), ('A', 'E', 'U'), ('A', 'I', 'A'), ('A', 'I', 'E'), ... ,('U', 'O', 'O'), ('U', 'O', 'U'), ('U', 'U', 'A'), ('U', 'U', 'E'), ('U', 'U', 'I'), ('U', 'U', 'O'), ('U', 'U', 'U')

...

- 길이 5 : ('A', 'A', 'A', 'A', 'A'), ('A', 'A', 'A', 'A', 'E'), ('A', 'A', 'A', 'A', 'I'), ('A', 'A', 'A', 'A', 'O'), ('A', 'A', 'A', 'A', 'U'), ('A', 'A', 'A', 'E', 'A'), ('A', 'A', 'A', 'E', 'E'), ('A', 'A', 'A', 'E', 'I'), ('A', 'A', 'A', 'E', 'O'), ('A', 'A', 'A', 'E', 'U'), ... ('U', 'U', 'U', 'U', 'U', 'U')

이 j들을 join 해주고, dictionary 배열 sorting만 해주면 된다.

LG Aimers에서 KAIST 신진우 교수님 강의를 듣고 정리한 내용입니다.

틀린 부분이 있다면 댓글 부탁드립니다!

1. Problem Setting

(1) Dimensionality Reduction

2차원 데이터가 있을때, x1과 x2 중에서 더 중요하다고 할 수 있는 데이터는 x1이다.

x1의 분산이 더 크기 때문이다.

이때, 차원을 축소하여 x1으로만 1차원으로 나타내어도, 데이터의 표현이 크게 달라지지 않는다.

고차원 데이터의 문제점으로는 다음과 같다.

- 분석 및 시각화의 어려움

- 가끔 overcomplete 되거나, 많은 차원들이 서로 중복되는 경우가 있음

compact data representation을 위해서 사용되는 대표적인 방법이 PCA (Principal Component Analysis, 주성분분석)이다.

예를 들어, 집값을 예측한다고 했을때 학습에 사용하는 피처를 5차원 (크기, 방 개수, 욕실 개수, 주변 상권, 범죄율)에서 2차원 (크기, 위치)으로 줄여 학습하면 더 효율적일 수 있다는 것이다.

(2) PCA Algorithm

1. 데이터의 평균으로 데이터를 빼서 원점 근처로 이동시킨다.

2. 데이터의 표준편차로 데이터를 나누어서 standardization 시킨다. 

이때, original data의 피처 차원은 D이다.

3. data의 covariance matrix (공분산 행렬)을 구하고, 행렬에 대해 M개의 largest eigen value를 구한다.

M은 차원 축소하고자 하는 차원으로 D >>> M 이다.

4. 3에서 구한 eigen vector로 정의된 공간으로 모든 데이터를 projection 한다.

5. projection한 데이터의 standardization, centering을 undo한다.

2차원 데이터를 PCA를 통해 1차원으로 차원 축소하는 과정이다.

(3) Data Matrix and Data Covariance Matrix

- N : sample 개수

- D : original data feature 개수

데이터 X (평균이 0)에 대해서 data matrix를 구하면 위와 같다.

이 데이터에 대해서 covariance matrix를 구해보면,

(4) Code : Low Dimensional Representation

데이터를 저차원 표현한 것을 code라고 부른다.

PCA 과정에서의 projection, subtraction, division은 모두 linear한 과정들이다.

이를 하나의 행렬 B로 linear transformation 했다고 한다면, 다음과 같이 나타낼 수 있다.

- x : 원본 데이터 (D차원)

- z : 변형 데이터 (M차원)

- B : 찾아야 할 행렬 (D x M차원), orthogonal matrix (B의 컬럼벡터들이 서로 수직이고 크기가 1)

결국, 행렬 B를 찾는 것이 PCA의 과정이다!

이를 Encoder와 Decoder의 관점에서 보면,

original data에 B를 곱해 코드 z를 만들고,

z에 B의 전치행렬을 곱하여 복원한다.

이때, B는 orthogonal matrix이므로 B의 전치행렬은 역행렬이다.

B의 전치행렬은 인코더, B는 디코더로 볼 수 있다.

예를 들어, MNIST 데이터셋에서 총 60,000개의 데이터가 있으며 (N = 60,000), 28 x 28 = 784 픽셀이 있을 때 (D = 784)

D를 2 또는 3차원으로 축소하여 데이터를 나타내는 것이 PCA, 즉 선형적 인코딩 과정인 것이다.

2. Maximum Variance perspective

(1) Idea

데이터 안의 '정보'란, 공간을 채우고 있는 것과 같다.

데이터가 얼마나 퍼저있는가 즉, 분산이 중요한 정보인 것이다.

X와 Y 중에서 더 중요한 피처는 X라고 말할 수 있는데, 그 이유는 분산이 더 크기 때문이다.

그러나, X와 Y 둘 중에서 하나만 골라서 사용하지 말고, 새로운 축을 구성하면 두 정보를 다 활용할 수 있다.

X, Y가 아닌 방향을 골라 그 방향으로 데이터를 projection하면서,

해당 방향으로의 분산이 최대가 될 수 있도록 한다면 데이터 활용이 더 커질 것이다.

(2) Matrix again

공분산 행렬의 고유벡터가 왜 데이터의 분산을 최대로 하는 방향인지에 대해 수학적으로 증명해본다.

- 목표 : 분산을 최대로 하는 orthogonal matrix B 찾기

- 결과 : 데이터의 공분산 행렬 S에 대한 M개의 고유값에 상응하는 고유벡터들은 행렬 B의 컬럼 벡터이다.

- 증명 방법 : 수학적 귀납법 (Induction)

1. n = 1

1차원 데이터에 대해 분산은 $\sigma ^2$이다.

공분산 행렬 S는 $\sigma ^2$ 자체이며, 이 값이 고유값이다.

고유벡터는 1차원에서 단위 벡터 [1]이고, 행렬 B도 [1]이다.

1차원 데이터의 경우, 공분산 행렬의 고유벡터는 단순히 데이터의 방향을 나타내는 단위 벡터이다.

강의에서는 다음과 같은 방식으로 증명하였다.

코드 z의 분산을 구하는 식은 첫 번째 식과 같다. 그리고 z는 b1과 데이터 x의 선형 결합으로 나타낼 수 있다.

분산을 구해보면 두 번째 식처럼 나오고, 그 식을 최대로 하는 b1을 convex optimization으로 구한다.

convex optimization의 objective function과 constraint (정규화를 해서 데이터의 분산을 최대화하는데 영향을 미치지 않도록 한다.)는 다음과 같다.

라그랑주 함수는 다음과 같고, 이를 KKT condition으로 푼다.

라그랑주 함수에 대해 b1에 대한 편미분을 수행하고, 이를 0으로 설정하여 구해보면

$S{b_1} = {\lambda_1}{b_1}$

따라서, 분산을 최대로 하기 위해서는 가장 큰 고유값의 고유벡터를 주성분으로 삼아야 한다.

2. n = k-1일 때 가정

n = k-1 차원에서 행렬 B의 컬럼 벡터들이 공분산 행렬 S의 고유벡터들이며,

행렬 B가 데이터의 분산을 최대로 하는 orthogonal matrix임을 가정하자.

3. n= k

동일하게 optimization problem으로 표현할 수 있다.

라그랑주 함수는 다음과 같다.

라그랑지안의 첫 번째 필요 조건은 gradient = 0이 되는 것이므로,

이제 임의의 $j \in \left\{ 1, ... ,k\right\}$에 대해 다음을 만족해야 한다.

이때 $b_j$는 S의 고유벡터이므로 $S{b_j} = {\lambda_j}b_j$ 이고 ${b_j^T}{b_i}=0$을 만족한다. 따라서,

이로부터 ${b_j^T}{b_{k+1}}=0$임을 알 수 있다.

식이 단순해지고 다음과 같이 표현된다.

따라서, $b_{k+1}$은 S의 고유벡터이며, 고유값은 $\lambda$이다.

4. 고유값의 순서

우리는 k번째 고유벡터까지 알고 있다고 했을 때, $b_{k+1}$은 k+1번째로 큰 고유값에 대응하는 고유벡터여야 한다.

그렇지 않으면, 고유값이 더 큰 고유벡터와의 직교 조건이 충족되지 않기 때문이다.

결론적으로, $b_{k+1}$도 S의 고유벡터이며, $b_1, b_2, ..., b_{k+1}$은 모두 직교한다.

3. PCA in High Dimensions

실제 데이터의 사례를 보면, 데이터의 개수가 데이터의 차원보다 더 적은 경우가 있다. (N << D)

예를 들면, 100 x 100 픽셀의 이미지에서의 D = 10,000 인데, 데이터의 개수 N = 100 인 경우가 있다.

이런 경우의 PCA는 다음과 같이 구할 수 있다.

${X^T}X \in R^{D \times D}$를 구하는 것보다

${X}{X^T} \in R^{N \times N}$을 구하는 것이 계산량이 더 적기 때문이다.

1. 차원 축소의 방법으로 PCA가 대표적이다.

2. 데이터의 공분산 행렬을 고유값 분해했을 때, 가장 큰 순서대로의 고유값에 해당하는 고유벡터가 주성분이 된다.